
Input the required dimensions and get to know the concrete material quantity and cost to purchase.
The concrete calculator is developed for estimating and planning concrete-related projects including (slabs, walls, columns, footings, stairs, and curbs).
The calculator provides an accurate measurements, considering factors such as length, width, depth, and quantity. Also enter the price to calculate the total volume and cost of materials when you enter the price per cubic foot, price per cubic yard, or price per cubic meter.
"The concrete is the special construction material that is prepared by composing of a mixture of cement, water, and aggregates such as sand, gravel, or crushed stone"
When the water and cement mix, they form a paste that coats the surface of the aggregates and binds them together into a solid, durable mass.
Let us take you through the formulas of the concrete volume required for constructing various structures.
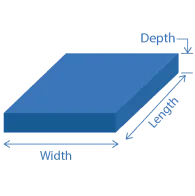
$$ Volume\left(ft^{3}\right) = Height * Length * Width $$
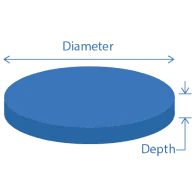
$$ Area\left(ft^{2}\right) = \pi * \left(\frac{Diameter}{2}\right)^{2} $$
$$ Volume\left(ft^{3}\right) = Depth * Area $$

$$ Volume\left(ft^{3}\right) = Height * Length * Width $$
.webp)
$$ Volume\left(ft^{3}\right) = Height * Length * Width $$
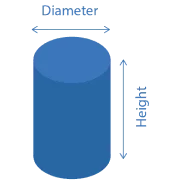
$$ Area\left(ft^{2}\right) = \pi * \left(\frac{Diameter}{2}\right)^{2} $$
$$ Volume\left(ft^{3}\right) = Height * Area $$
.webp)
Keep in mind that:
$$ \text{Volume Under Platform} \left(ft^{3}\right) = Width * \text{Platform Depth} * \left(\text{Rise Height} * \text{No. Of Steps}\right) $$
Now ignoring the platform, we will only focus on the steps. In the picture above, we have four steps. Now we have:
$$ \text{Volume Under Each Step}\left(ft^{3}\right) = \text{Run Depth} * Width * \left(\text{Rise Height} * \text{Step Number}\right) $$
$$ \text{Total Volume} \left(ft^{3}\right) = \text{Volume Under Platform} \left(ft^{3}\right) + \text{Volume Under Each Step} $$
.webp)
Here we will again determine the volume of the concrete from the bottom step to the top one. We have two sections here that are curb and gutter, respectively.
$$ \text{Volume Under Curb} \left(ft^{3}\right) = \text{Curb Depth} * Length * \left(\text{Curb Height} + \text{Flag Thick\ckness}\right) $$
$$ \text{Volume Under Gutter} \left(ft^{3}\right) = \text{Gutter Width} * Length * \text{Flag Thickness} $$
$$ \text{Total Volume} \left(ft^{3}\right) = \text{Volume Under Curb} \left(ft^{3}\right) + \text{Volume Under Gutter} \left(ft^{3}\right) $$
Let us have a look of the following types of the concrete below along with their densities:
| Type | Density (kg/m³) |
| Ordinary | 2400 |
| Light Weight | <1920 |
| High Density | 3000-4000 |
| Reinforced | 2500 |
| Precast | 2400 |
| Prestressed | 2330 |
| Air-Entrained | 2535 |
| Glass | 2620 |
| Rapid Hardening | 2250 |
| Asphalt | 1950 |
| Lime | 2080 |
| Roller Contracted | 2400 |
What about if we resolve an example here? Yes, we are going to do so that you understand what we are discussing exactly. Let us go!
A contractor has started a project in which about 5000 concrete circular slabs are needed. The diameter of the slab is about 2ft and expected depth is about 5 inches. How to figure concrete required to make 5000 circular slabs?
Answer:
$$ Area\left(ft^{2}\right) = \pi * \left(\frac{Diameter}{2}\right)^{2} $$
$$ Area\left(ft^{2}\right) = 3.14 * \left(\frac{2}{2}\right)^{2} $$
$$ Area\left(ft^{2}\right) = 3.14ft^{2} $$
$$ Volume\left(ft^{3}\right) = Depth * Area $$
$$ Volume\left(ft^{3}\right) = 5 * 3.14 $$
$$ Volume\left(ft^{3}\right) = 15.14ft^{3} $$
Concrete Calculator determines concrete quantity for construction. Enter the dimensions of a slab, base, pillar, or structure and it computes the required amount of material, hence diminishing the volume expended and superfluous expenses.
The calculator needs you to put numbers for how long, how wide, and how deep the space is that gets the concrete. It then amplifies these figures to ascertain the capacity and translates them into cubic yards, cubic meters, or sacks of concrete required.
Using a specific measurement tool for mixing cement can help you choose the correct quantity, avoiding running out or having too much left over. It facilitates financial planning, preventing frivolous spending, and simplifying the building procedure.
Absolutely, numerous Concrete Complementors offer a calculation of the required quantity of bags for the chosen concrete blend. This helps in better material planning and cost estimation.
Most calculators provide results in cubic meters, cubic feet, and cubic yards. Some also permit transformations into tons or sacks of concrete, based on the project’s requirements.
Absolutely, it measures amounts of concrete needed for various types of projects, such as simple floors, strong base structures, or very heavy-duty uses. The kind of cement can influence the mass and quantity of containers needed.
A Solid Structurer offers an estimate, however precision relies on precise data input. To increase accuracy, always include a slight fraction for impurities and possible fluctuations in the blend.
Undoubtedly, certain Concrete Calculators permit arithmetic for an array of forms, including cylinders, footings, or asymmetrical constructions. If necessary, dismantle intricate patterns into fragmented units and compute the aggregate space.
To convert cubic meters to cubic yards, multiply by 1. 307. Conversely, to convert cubic yards to cubic meters, multiply by 0. 7646. Many online calculators provide this conversion automatically.
A Concrete Calculator aids hobbyist builders in determining concrete quantities precisely for diverse applications, optimizing resource use and curtailing excess expenditure.